Сущность финансовой пирамиды
Финансовая пирамида (Financial Pyramid) - это такая структура, в которой профит извлекается путем формирования денежных поступлений от привлечения все большего количества инвесторов.
Все финансовые пирамиды обычно подразделяют на 2 типа:
- многоуровневые пирамиды по схеме снежный ком или лавина;
- схемы Понци.
1) Многоуровневая пирамида
Советский популяризатор науки Я. И. Перельман в своей книге «Живая математика» еще в 1967 г. описал вариант «пирамиды» как организацию акции, имевшую место в дореволюционной России, по покупке велосипедов путем «веерного» сбора денег по переписке.
В настоящее время эта схема основана на том, что каждый новый участник пирамиды, новичок, сначала делает свой входной взнос. Этот взнос сразу же делится между участником, пригласившим новичка, а также теми, кто пригласили пригласившего, т.е. более ранними участниками пирамиды. После вступительного взноса, новичок должен пригласить еще двух или больше человек, вступительные взносы которых уже пойдут в его пользу и в пользу более ранних участников. Так продолжается из уровня в уровень.
Рассмотрим упрощённый принцип работы такой пирамиды на примере аферы с велосипедами в дореволюционной России.
В газете печаталась яркая реклама «Велосипед за 10 руб», когда его рыночная цена, допустим – 50 руб. (в наше время таким примером может служить покупка iphone или иной вещи по цене в разы ниже рыночной, обычно через объявления или сайты в сети Интернет).
Немало людей, заинтересовались заманчивым предложением объявлением и просили прислать условия необычной покупки. В ответ на запрос они получали подробный проспект, из которого узнавали следующее.
За 10 руб. высылался пока не самый велосипед, а только 4 билета, которые надо было сбыть по 10 руб. своим четверым знакомым. Собранные таким образом 40 руб. следовало отправить фирме, и тогда лишь прибывал велосипед.
Эти четверо должны сбыть свои билеты 4*5, т.е. 20 другим, убедив их в выгодности такой покупки. Допустим, что это удалось, и 20 покупателей завербовано. Лавина движется дальше: 20 новых обладателей билетов должны наделить ими 20*5=100 других.
До сих пор каждый из «родоначальников» лавины втянул в нее 1+4+20+100=125 человек, из которых 25 имеют по велосипеду, а 100 — только надежду его получить, уплатив за эту надежду по 10 руб. Далее цепочка продолжается до того предела, когда желающих приобрести велосипед не останется и последний уровень останется с никому ненужными билетами стоивших им по 10 руб.
Какой же числовой ряд получается?
1 = 1
4 = 1*4 или * 5 для каждого последующего уровня
20 = (1+4)*4 4*5=20, 20*5=100 и т.д.
100 = (1+4+20)*4
500 = (1+4+20+100)*4
2500 = (1+4+20+100+500)*4
12500 = (1+4+20+100+500+2500)*4
….. и т.д.
Формулу можно записать в следующем виде
Q = ∑ (n1+n2+n3+…+nn)*4
Q – количество участников пирамиды.
В нашем случае, то количество новых участников, которое необходимо привести – 5, определяет доходность пирамиды – 400 %, если их нужно было привести 6 человек, то доходность была бы, соответственно, – 500 % и т.д.
Допустим, каждому участнику необходима 1 неделя для поиска новых участников и реализации имеющих 5 билетов. Таким образом, новый уровень формируется за одну неделю.
Если будет известно, что желающих купить велосипеды на данной территории 1 млн человек, то путем нехитрых вычислений можно прийти к выводу, что они смогут обеспечить только 200 тыс. человек велосипедами, а остальные 800 тыс. человек не получат ничего. Т.е. участники, начиная с 200001 потратят деньги на простые бумажки в виде билетов.
Остается вопрос, через какой промежуток времени произойдет полное насыщение пирамиды и ее предел. Для этого нужно просто продолжить числовой ряд, на формирование каждого звена которого уходи приблизительно 1 неделя. В нашем случае получим, что до окончания 9 недели (через 2 месяца) пирамида рухнет.
2) Суть пирамид по схеме Понци в том, что ее организатор приглашает участников вложить деньги и при этом обещает очень высокий и часто «гарантированный» доход по прошествии небольшого срока. При этом не нужно привлекать новых участников — нужно просто ждать. Первым немногочисленным участникам организатор выплачивает высокие проценты дохода из своих личных средств, после чего обычно слухи о «работающей» схеме с отличной доходностью распространяются, и новые вкладчики сами идут к организатору. Дальше организатор просто расплачивается со старыми вкладчиками денежными средствами, которые поступают от новых — игра «в мешок» работает. Понятно, что по мере того как первые участники действительно получают обещанные доходы, количество желающих растет, а кроме того и старые участники начинают вкладывать повторно — организатор испытывает увеличение притока средств.
Финансовая пирамида под названием схема Понци заканчивается по простой причине: каждый вкладчик ожидает получить больше, чем вложил, в то время как других доходов, кроме этих вкладов, организатор не получает -таким образом схема обречена на крах. Обычно это лучше всего понимает сам организатор, поэтому зачастую в тот момент, когда поток новых вкладчиков начинает «ослабевать», организатор присваивает все уже сделанные вклады и скрывается.
Пытаясь предугадать крах подобной пирамиды, прибегнем к помощи математического моделирования.
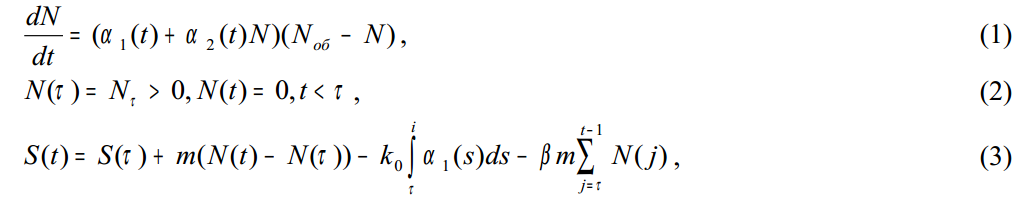
где N(t) – общее число клиентов финансовой пирамиды в момент времени t; Nоб – общее число потенциальных клиентов; α1 (t) – интенсивность рекламной кампании; α2 (t) - степень общения клиентов между собой; m - сумма вклада; β - процент годовых, ежемесячно начисляемый на каждый вклад; k0 - коэффициент пропорциональности расходов на рекламу; S(t) - сумма, собираемая финансовой пирамидой.
Явная формула (3) для функции S(t) удобна для математического исследования и построения упрощенных моделей. Математическая модель позволят проводить имитационное моделирование деятельности финансовой пирамиды, рассчитывать время существования пирамиды и время разорения, ставки процента, расходов на рекламу и др.


